Betrachtet man einen zylinderförmigen Permanentmagneten, so gibt es keine freien Ströme oder zeitveränderliche elektrische Felder, daher gilt:
$$ \overrightarrow{\nabla} \times \overrightarrow{H} = 0 $$
Dies is gleichbedeutend damit, dass \(\overrightarrow{H}\) als Gradient eines Potentials \(\Phi\) geschrieben werden kann:
$$ -\overrightarrow{\nabla} \Phi = \overrightarrow{H} $$
Außerdem hat die magnetische Flussdichte keine Quellen:
$$ \overrightarrow{\nabla} \cdot \overrightarrow{B} = 0 $$
Magnetische Flussdichte, magentisches Feld und Magnetisierung sind über folgende Gleichung verknüpft:
$$ \overrightarrow{B} = \mu_0 (\overrightarrow{H} + \overrightarrow{M}) $$
Bildung der Divergenz auf beiden Seiten des Gleichheitszeichen führt zu:
$$ div\overrightarrow{H} = -div\overrightarrow{M} $$
Substituiert man anschließend den Potentialansatz für \(\overrightarrow{H}\) erhält man:
$$ div(\overrightarrow{\nabla}\Phi) = div\overrightarrow{M} $$
Diese Gleichung entspricht einer Poissongleichung:
$$ \Delta \Phi = div \overrightarrow{M} $$
Ähnlich dem Vorgehen beim elektrostatischen Fall, kann diese Differentialgleichung mit einer Greenschen Funktionen gelöst werden. Die allgemeine Lösung ist:
$$ \Phi(\vec{r}) = -\frac{1}{4\pi} \int \frac{div(\overrightarrow{M})}{|\vec{r}-\vec{r'}|} dV' $$
Dabei geht die Integration über das Volumen des Magneten.
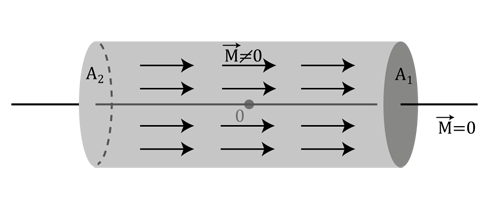
Abbildung 1 zeigt den Magneten. Die Magnetisierung sei innerhalb des Magneten konstant \( \vec{M}=\begin{pmatrix} M_x \\ 0 \\ 0 \end{pmatrix} \) und außerhalb \(0\). Sie ändert sich also an den Polflächen, wo dementsprechend Quellen der Magnetisierung sitzen. Für die weitere Berechnung muss daher der Ausdruck der Divergenz in einen Ausdurck für die Oberflächendivergenz umgewandelt werden. Die Integration muss dann nur noch über die Polflächen ausgeführt werden.
Abbildung 1 zeigt weiterhin, dass an der rechten Grenzfläche \(A_1\) die Magnetisierung vom Wert \(M_x\) auf \(0\) absinkt. An der linken Grenzfläche \(A_2\) ist es genau andersherum. Daraus folgt für die Flächendivergenzen:
$$ div_{surf}(\vec{M})|_{A_1} = -M_x \\ div_{surf}(\vec{M})|_{A_2} = M_x $$
So ergibt sich (für nähere Informationen siehe z.B. Kemmer, 1977):
$$ \Phi(\vec{r}) = -\frac{1}{4\pi} \int_{A_1} \frac{-M_x}{|\vec{r}-\vec{r'}|} dA' -\frac{1}{4\pi} \int_{A_2} \frac{M_x}{|\vec{r}-\vec{r'}|} dA' $$
\( \vec{r} \) ist der Ortsvektor zum Punkt, an dem man das Feld berechnet werden soll, \( \vec{r'} \) ist ein Ortsvektor zu einem Punkt auf der Polfläche des Magneten. Wegen der Symmetrie des Magneten ist es sinnvoll, nach Zylinderkoordinaten zu intergrieren.
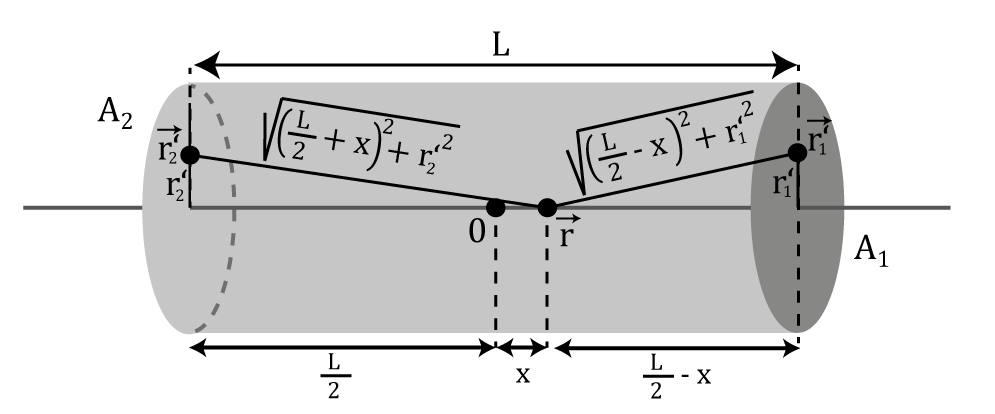
Abbildung 2 zeigt, wie der Ausdruck \( |\vec{r}-\vec{r'}| \) für die beiden Polflächen umparametrisiert werden muss. Es folgt:
$$ \Phi(x) = \frac{1}{4\pi} \int_{0}^{2\pi}d\phi \int_{0}^{R}dr'_1 r'_1 \frac{M_x}{\sqrt{(\frac{1}{2}L - x)^2+{r'_1}^2}} - \frac{1}{4\pi} \int_{0}^{2\pi}d\phi \int_{0}^{R}dr'_2 r'_2 \frac{M_x}{\sqrt{(\frac{1}{2}L + x)^2+{r'}_2^2} } $$
Mit dem Zusammenhang \( \int_{a}^{b} dr \frac{r}{\sqrt{c + r^2}} = \sqrt{c+r^2}|^b_a \) kann das Integral ausgerechnet werden:
$$ \Phi(x) = \frac{1}{2}M_x \left( \left[\sqrt{(\frac{1}{2}L - x)^2+{r'_1}^2} \right] _0^R \right) - \frac{1}{2}M_x \left( \left[\sqrt{(\frac{1}{2}L + x)^2+{r'_2}^2} \right] _0^R \right) $$
$$ \Phi(x) = \frac{1}{2}M_x \left( \sqrt{(\frac{1}{2}L - x)^2 + R^2} - \sqrt{(\frac{1}{2}L-x)^2} - \sqrt{(\frac{1}{2}L+x)^2 + R^2} + \sqrt{(\frac{1}{2}L+x)^2} \right) $$
Also:
$$ \Phi(x) = \frac{1}{2}M_x \left( \sqrt{(\frac{1}{2}L - x)^2 + R^2} - \left|\frac{1}{2}L-x\right| - \sqrt{(\frac{1}{2}L+x)^2 + R^2} + \left|\frac{1}{2}L+x\right| \right) $$
Aus \( \Phi(x) \) kann jetzt \( \vec{H} \) entlang der x-Achse berechnet werden:
$$ \vec{H}(x) = -\vec{\nabla}\Phi(x) = -\frac{\partial}{\partial x} \Phi(x) \vec{e}_x \\ $$
$$ =-\frac{1}{2}M_x \left( - \frac{\frac{1}{2}L-x}{\sqrt{(\frac{1}{2}L-x)^2 + R^2}} + \frac{\frac{1}{2}L-x}{\sqrt{(\frac{1}{2}L-x)^2}} - \frac{\frac{1}{2}L+x}{\sqrt{(\frac{1}{2}L+x)^2 + R^2}} + \frac{\frac{1}{2}L+x}{\sqrt{(\frac{1}{2} L+x)^2}} \right) \vec{e}_x $$
$$ =-\frac{1}{2}M_x \left( - \frac{\frac{1}{2}L-x}{\sqrt{(\frac{1}{2}L-x)^2 + R^2}} + \frac{\frac{1}{2}L-x}{\left|\frac{1}{2}L-x\right|} - \frac{\frac{1}{2}L+x}{\sqrt{(\frac{1}{2}L+x)^2 + R^2}} + \frac{\frac{1}{2}L+x}{\left|\frac{1}{2} L+x\right|} \right) \vec{e}_x $$
Für Punkte \( \vec{r} \) außerhalb des Magneten ist \( |x|>\frac{L}{2} \). Daraus folgt:
$$ \vec{H}(x) =\frac{1}{2}M_x \left( \frac{\frac{1}{2}L-x}{\sqrt{(\frac{1}{2}L-x)^2 + R^2}} + \frac{\frac{1}{2}L+x}{\sqrt{(\frac{1}{2}L+x)^2 + R^2}} \right)\vec{e}_x $$
Für Punkte innerhalb des Magneten ist \( |x| \lt \frac{L}{2} \) und somit:
$$ \vec{H}(x) =\frac{1}{2}M_x \left( \frac{\frac{1}{2}L-x}{\sqrt{(\frac{1}{2}L-x)^2 + R^2}} + \frac{\frac{1}{2}L+x}{\sqrt{(\frac{1}{2}L+x)^2 + R^2}} -2 \right)\vec{e}_x $$
Für die magnetische Flussdichte außerhalb des Magneten gilt der Zusammenhang \( \vec{B}=\mu_0 \vec{H} \) und somit:
$$ \vec{B}(x) =\frac{1}{2}M_x\mu_0 \left( \frac{\frac{1}{2}L-x}{\sqrt{(\frac{1}{2}L-x)^2 + R^2}} + \frac{\frac{1}{2}L+x}{\sqrt{(\frac{1}{2}L+x)^2 + R^2}}\right)\vec{e}_x $$
Die Formel beschreibt aber auch die magnetische Flussdichte innerhalb des Magneten. Dies ist ersichtlich aus dem Zusammenhang \(\vec{B} = \mu_0 (\vec{H} + \vec{M}) \) und der Formel für \(\vec{H}(x)\) im Inneren des Magneten (siehe auch Sommerfeld, 1956).
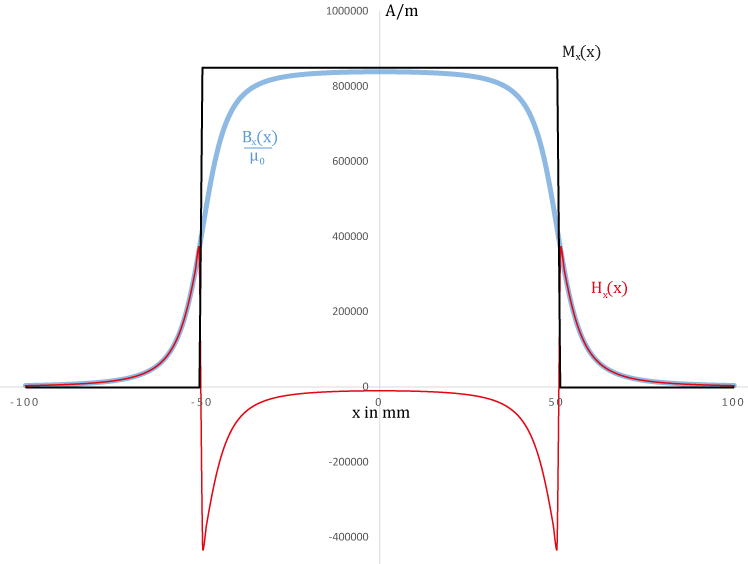
Der im Experiment verwendete Magnet hat die Länge \( L=100mm \) und Radius \( R=7.5mm \). Abbildung 3 zeigt für eine Magnetisierung von \( M_x(x)|_{-\frac{L}{2} \leqslant x \leqslant \frac{L}{2}} = 850\frac{\mathrm{kA}}{\mathrm{m}} \) den Graph der Magnetisierung, der magnetischen Feldstärke und der magnetischen Flussdichte. Zur Darstellung im Diagramm wurde die magnetische Flussdichte zuvor durch die magnetische Feldkonstante \(\mu_0\) geteilt.